Formula To Find Diameter Of Circle With Circumference Is Known

As with triangles and rectangles, we can attempt to derive formulas for the area and "perimeter" of a circle. Calculating the circumference of a circle is not as easy as calculating the perimeter of a rectangle or triangle, however. When the formula for calculating the circumference of a circle is used, the circle's radius is considered. As a result, the radius or diameter value must be known to calculate the circle's perimeter or circumference. Blame Welsh mathematician William Jones for the trouble pi causes you.

In 1706 Jones used the Greek word for circumference, περιϕέρεια, and shortened it to its first letter, π. As for π in circles, we have no one to blame but the marvel that is mathematics. Pi, or π, is the irrational number that links every circle's circumference to diameter and radius. To calculate the diameter of a circle, multiply the radius by 2.

If you don't have the radius, divide the circumference of the circle by π to get the diameter. If you don't have the radius or the circumference, divide the area of the circle by π and then find that number's square root to get the radius. Then, you can just multiply the radius by 2 to find the circle's diameter. The learning outcome of this article is that one can calculate the circumference of circular objects and circular paths. The diameter of a circle is twice to that of the radius.

If the diameter or radius of a circle is given, then we can easily find the circumference. We can also find the diameter and radius of a circle if the circumference is given. We round off to 3.14 in order to simplify our calculations.

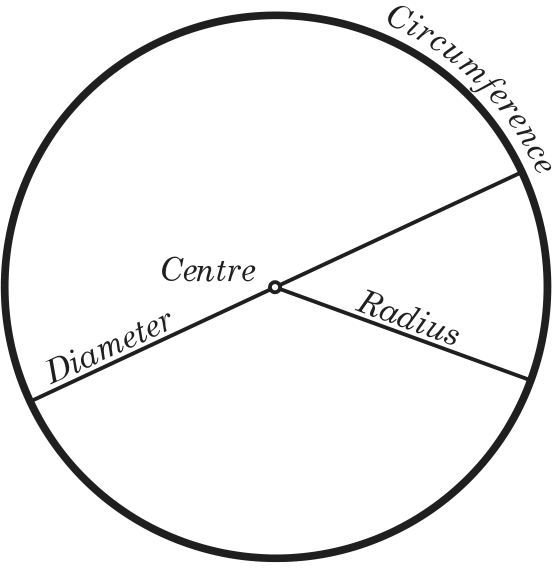
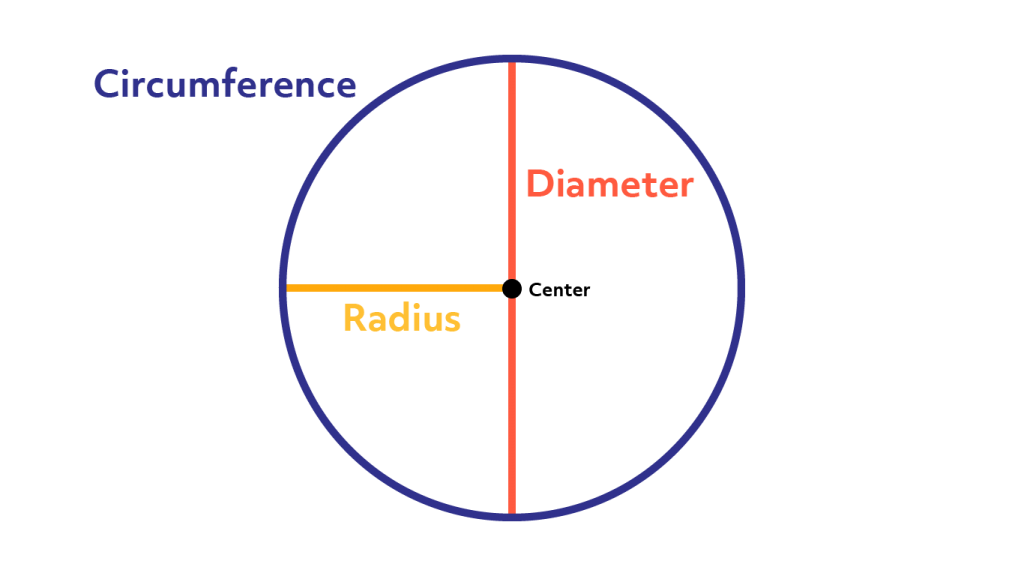
Circumference, diameter and radii are calculated in linear units, such as inches and centimeters. A circle has many different radii and many different diameters, and each one passes through the center. The radius, the diameter, and the circumference are the three defining aspects of every circle.

Given the radius or diameter and pi you can calculate the circumference. The diameter is the distance from one side of the circle to the other at its widest points. The diameter will always pass through the center of the circle.

You can also think of the radius as the distance between the center of the circle and its edge. Use the circle circumference formula to calculate the circumference of the following circles. That are not reused after they are calculated. This is in contrast to infinite series or iterative algorithms, which retain and use all intermediate digits until the final result is produced. Using geometrical formulas and equations gets easier with practice.

Ask for help from someone who has worked with circles or any other geometrical figures. You're likely to find that questions of geometry will seem less challenging with a little experience. Π is simply a ratio between the diameter, d of a circle and it's circumference. In other words, a circle that has a diameter of 1 or a radius of 1/2 will have a circumference of π.

Π is conveniently also the ratio of r squared to the area of the circle, meaning that a circle with radius 1 will have an area of π. Its diameter is 57.28 feet the formula of circumference of circle is 2 pi r , from this calculate... Circumference is in essence the distance or length around a circle. _, correctly pronounced like pie, is an irrational number, which means that it cannot be written as a fraction. So to be sure, a good approximation of π is 3.14 when used in particular formulas. Second, since no transcendental number can be constructed with compass and straightedge, it is not possible to "square the circle".

In other words, it is impossible to construct, using compass and straightedge alone, a square whose area is exactly equal to the area of a given circle. Squaring a circle was one of the important geometry problems of the classical antiquity. Amateur mathematicians in modern times have sometimes attempted to square the circle and claim success—despite the fact that it is mathematically impossible.

The circumference of the circular water pit is 18 feet. How can Marcus use this information to determine how long the beam needs to be to go across the center of the pit? Marcus needs to figure out the diameter of the pit. To understand how to calculate circumference we must first begin with the definition of circumference. Circumference of a circle is linear distance around outer border of a circle. To find out the circumference, we need to know its diameter which is the length of its widest part.

The diameter should be measured in feet for square footage calculations and if needed, converted to inches , yards , centimetres , millimetres and metres . Circumference refers to the distance around a circle. It is a one-dimensional measurement of any two-dimensional circular surface's boundary. The circle's radius is also taken into account to find the circle's circumference. Thus, to calculate the perimeter of a circle, we must first determine the radius or diameter of that circle. The circumference is the measurement of the circle's boundaries.

When we cut open a circle and draw a straight line through it, this length is known as its circumference or the perimeter. It is commonly expressed in units like centimeters, meters, or other relevant units of length. As stated before, the perimeter or circumference of a circle is the distance around a circle or any circular shape. The circumference of a circle is the same as the length of a straight line folded or bent to make the circle. The circumference of a circle is measured in meters, kilometers, yards, inches, etc. Once again in this example, we're given the radius of the circle.

Although it's not a clean number like our previous example, but we can still simply plug the number directly into the formula like what we did above. Be aware of the units that this circle's radius is given in and remember to give your final answer in the same unit. In this question, we find that the circumference is equalled to 53.41m. Lauren is planning her trip to London, and she wants to take a ride on the famous ferris wheel called the London Eye.

While researching facts about the giant ferris wheel, she learns that the radius of the circle measures approximately 68 meters. What is the approximate circumference of the ferris wheel? The diameter of a circle can be calculated according to the given parameters. If the parameters like radius, circumference, or area are given then we can directly use the following formulas.

Formula To Find Diameter Of A Circle From Circumference The diameter is defined as twice the length of the radius of a circle. This tool will calculate the diameter of a circle from the circumference, and will convert different measurement units for circumference and diameter. Acircleis a closed round shape with all the points equidistant from a fixed point known as the centre.

The circle's circumference is measured in length units such asmetresandcentimetres. Similarly, we come across more circular shapes in our everyday life like a dinner plate, Ferris wheel, the dial of a clock, cricket ground, candy, steering wheel, etc. If a circle's circumference is known, then use the inverse of the circumference formula to solve the radius.

The iterative algorithms were independently published in 1975–1976 by physicist Eugene Salamin and scientist Richard Brent. As modified by Salamin and Brent, it is also referred to as the Brent–Salamin algorithm. Thus, we can calculate the circumference of a circle if we know the circle's radius . For most calculations that require a decimal answer, estimating π as 3.14 is often sufficient.

For instance, if a circle has a radius of 3 meters, then its circumference C is the following. Not just this but there are some significant distances on a circle that needs to be calculated before finding the circumference of the circle. Diameter is the distance from one side of the circle to the other, crossing through the center/ middle of the circle.

The perimeter and area of triangles, quadrilaterals , circles, arcs, sectors and composite shapes can all be calculated using relevant formulae. Calculating the circumference of a circle is the most accurate way to determine it. The radius of the circle must be known for this method. The figure below shows a circle with radius R and center O. You can think of it as the line that defines the shape. For shapes made of straight edges this line is called theperimeter but for circles this defining line is called the circumference.

The circumference's ratio to its diameter is fixed in any circle drawn with any radius. This ratio is represented using the Greek letter . If we take any circular objects around us and find the ratio of the circumference to its diameter, it is always a fixed constant (\pi ). The Circumference of a circle is the distance around the outside of it . The circumference is equal to π times the twice the radius or the diameter .

Determining the circumference of a circle can be compared to determining the perimeter of any polygon. The circumference is simply the distance around the outside of the circle. If you know the circumference, radius, or diameter of a circle, you can also find its area. Area represents the space enclosed within a circle.

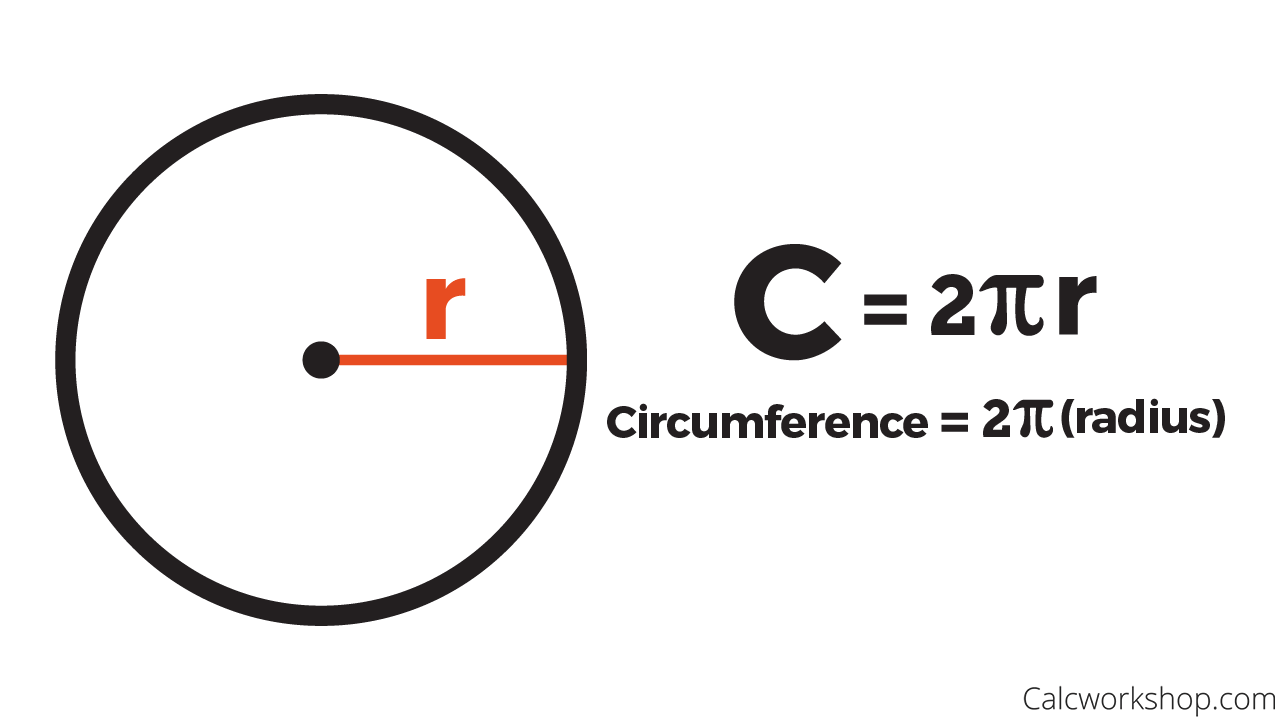
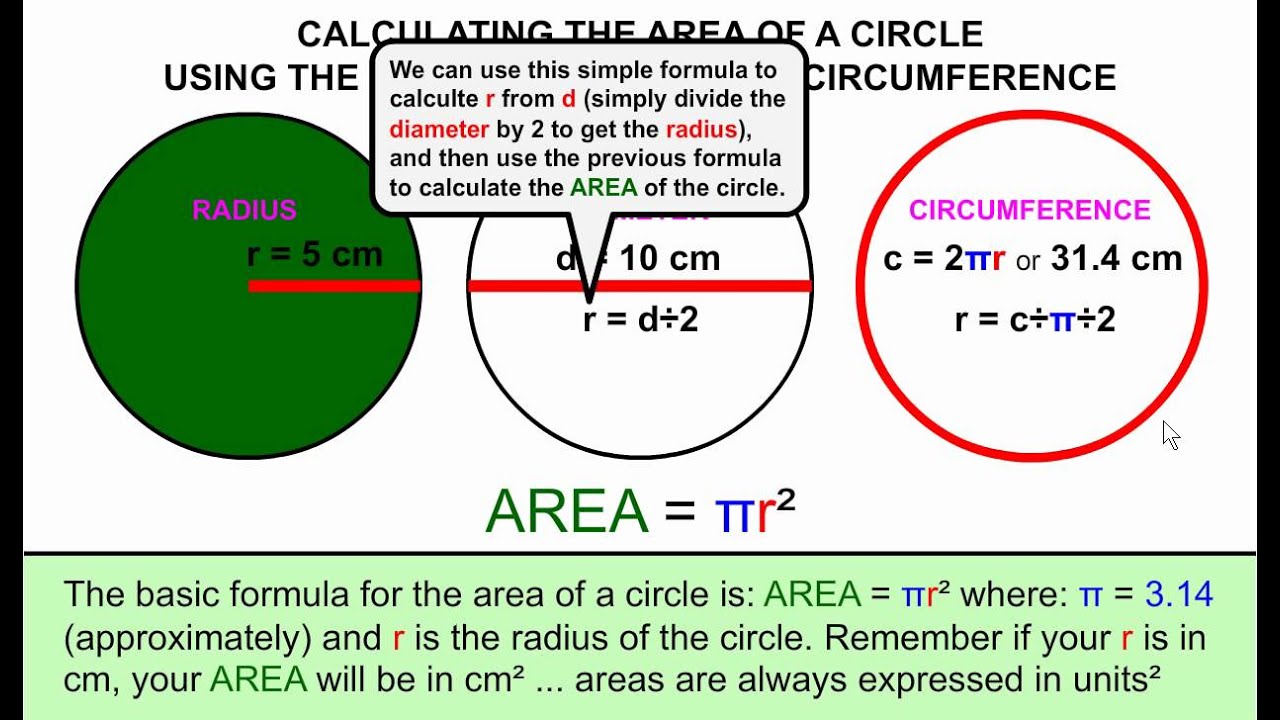
It's given in units of distance squared, such as cm2 or m2. The circumference of a circle C is equal to 2 times pi times the radius r. The area of a circle A is equal to pi times the radius r squared.

You can then use this line accordingly, or the radius, alongside with π in order to calculate the circumference. All you need to do is multiply the radius by 2 to obtain the diameter. Because finding the exact center may prove difficult, it's best to take several measurements to ensure accuracy. For simplicity, we'll use the former approach. Thus, a circle is simply the set of all points equidistant from a center point . The distance r from the center of the circle to the circle itself is called the radius; twice the radius is called the diameter.

The radius and diameter are illustrated below. This proportion of circumference to diameter is the description of the constant pi. It is used in different areas, such as physics and mathematics.

The radius 'r' of the circle and the value of 'pi' can determine the circumference of a circle formula. There are two ways of finding the perimeter or circumference of a circle. The first formula involves using the radius, and the second involves using the diameter of a circle. It is important to note that both two methods yield the same result. Fizzywoz - If you look at examples #1-#4 at the end of the article you can see how numbers are plugged into the equation.

You will usually just plug in a known radius into the equation to figure out the circumference or you may plug in a known circumference to determine the radius. The diameter of a circle is a segment whose endpoints lie on the circle and whose midpoint is the center of the circle. When someone says 'lie on the circle,' that means on the outline that traces the circle, not the space within that outline. The center of the circle is a point exactly in the middle of the space within the outline. The center is also the same distance away from every point on the outline of the circle. The distance from the center to a point on the circle is called a radius.

To find the diameter of a circle, multiply the circle's radius by two. Learn the definition of a diameter and a radius and review a detailed explanation of the formula used to find the diameter of a circle with examples. Now to practice, try drawing a circle on a piece of paper, and measure your diameter with a ruler. The "diameter" is any straight line that passes through the center of the circle, where both end points of the line lie on the circle circumference. We come across many shapes in our daily lives, but the circle's most commonly used shape.

The length of their boundary is the circumference of that coin. The circumference of any object in mathematics specifies the route or border that surrounds the object. In other words, Thecircumference of a circleis the circle's perimeter. • We know that the area of a circle is π times the radius squared or ( 3.14 x r2). Where d is the diameter of the circle, r is its radius, and π is pi.

Write a C program to input radius of a circle from user and find diameter, circumference and area of the circle. How to calculate diameter, circumference and area of a circle whose radius is given by user in C programming. Logic to find diameter, circumference and area of a circle in C. To calculate the circumference of a circle, you must first have at least one other measurement, such... The trigonometric functions rely on angles, and mathematicians generally use radians as units of measurement. There also exist non-circular smooth curves of constant width.